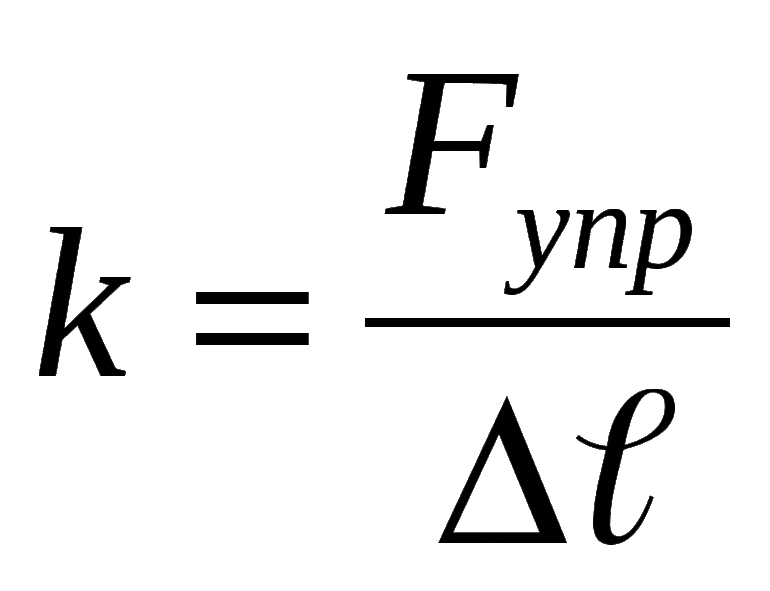Содержание
В физике закон Гука, формула и определение устанавливают причины и последствия поведения упругих тел и доказывают, что деформация — это линейная функция напряжения. Закон действует не на все материалы, даже те, которые считаются эластичными, например, резина, не подчиняющаяся ему, поскольку материалы, на которые воздействует упругость, должны прежде всего обладать сложной кристаллической решеткой.
История открытия
Закон жесткости был сформулирован в 1676 году известным британским ученым физиком Робертом Гуком. Он занимал должность профессора Лондонского университета и одновременно секретаря Лондонского королевского общества и считался академическим соперником Ньютона. Вместе с другим известным ученым Робертом Бойлем он стал автором усовершенствованного воздушного насоса.
Кроме того, Гук считается автором различных теорий волновой оптики, разработчиком первого григорианского микроскопа, который имел расширение в 30 раз больше, чем у самого мощного аналогичного аппарата того времени. Он увлекался биологией и первым описал клетку. Ученый также специализировался на палеонтологии, геологии и астрономии.
В 1665 году англичанин Роберт Гук опубликовал удивительную книгу под названием «Микрография», в которой описывались взгляды на мир, невидимого невооруженным взглядом. В это время автору было 30 лет, а книга стала первой публикацией Лондонского королевского общества и первым научным бестселлером.
Позже Сэмюэль Пепис, автор знаменитого дневника о повседневной жизни лондонцев периода Стюартовской Реставрации назвал ее самой гениальной книгой, которую он когда-нибудь читал в своей жизни. Примечательно, что Гук сам сделал иллюстрации к книге, показывая том, что он видел через микроскоп, который сам соорудил.
Определение и формула
Закон упругости, является физическим принципом упругого поведения твердых тел. Определение его состоит в том, что смещение или деформация, испытываемые объектом, подвергающимся воздействию силы, будут прямо пропорциональны деформирующей силе или нагрузке.
Он моделирует деформацию твердого тела при приложении внешнего напряжения, тяги или сжатия и устанавливает связь между удлинением металла, например, напряжением fупр, приложенным к нему.
С другой стороны, особенность этого закона учитывает два основных параметра:
- линейность, которая измеряется пропорционально удлинению в зависимости от приложенного усилия;
- упругость, которая указывает на обратимость растяжения, возникающей в результате принуждения.
В законе упругости эти два понятия не зависят друг от друга. Когда эластичность нарушена, он не будет применим к материалу.
Кратко основная формула закона упругости может записываться:
F = -К*Х,
где:
- F — деформирующая сила;
- Х — длина сжатия или удлинения;
- К — константа пропорциональности, называемая пружинной константой, обычно выражаемая в Ньютонах на метр, Н/м.
Для расчета «Х» необходимы два измерения: начальная (L0) и конечная длина (Lf). ΔL= Lf-L0 — изменения длины, то есть фактическая деформация. Следовательно, обобщенная формула заключается в следующем:
F = -К * ΔL
Эластичная потенциальная энергия — это энергия, сохраненная в объекте, которая растягивается, сжимается, скручивается или изгибается. Уравнение упругой потенциальной энергии имеет вид:
U=½*К*Х²,
где
- U — упругая потенциальная энергия;
- К — константа пропорциональности;
- Х — длина сжатия или удлинения.
Когда ΔL = 0, пружина находится в положении равновесия. Это уравнение работает только на линейной пружине, которую толкают исключительно в одном направлении, например, влево или вправо, вверх или вниз.
Угловая частота колебания пружины
Применение закона Гука для расчета упругости может использоваться и для пружин, и для упругих тел. Для первой конструкции применяется «уравнение пружины», которое является наиболее общей формулировкой закона Гука, «К» является постоянной упругости пружины и зависит от ее длины и состава.
Помимо этого, можно рассчитать угловую частоту колебаний пружины (ω), используя массу груза, вызывающего его растяжение (m). Для этого применяют следующие формулы:
ω = 2 πf
К = F/Δl
m =1/3m пружины + m тела
ω = √ К/М,
где:
- К — коэффициент упругости, Н/м;
- F — сила деформации, Н;
- Δl — изменение формы, м;
- f — линейная частота, Гц;
- m — масса, кг;
- T — период колебания, сек.
Расчет упругости должен учитывать сложное распределение натяжения в телах. Для этого применяются уравнения Ламе — Гука, которые имеют конкретные формулы для твердого тела в соответствии от его конкретной формы: одномерной, трехмерной изотропной или трехмерной ортотропной.
Точка текучести
Тщательно проведенные эксперименты, доказывающие закон упругости, показывают, что, например, для мягкой стали и железа молекулы проволоки начинают «скользить» после того, как нагрузка превышает предел упругости, то есть материал становится пластичным. На это указывает небольшой «излом» в графике, который называется пределом текучести материала.
Переход от упругой к пластической стадии проявляется при внезапном удлинении, и когда нагрузка увеличивается, удлинение быстро растет, после чего происходит ее разрыв. Разрушающее напряжение проволоки представляет собой соответствующую силу на единицу площади поперечного сечения.
Прочность и пластичность металла, и его способность удлиняться, зависят от дефектов кристаллической решетки. Они могут состоять из отсутствующего атома в узле или дислокации в плоскости атомов. Пластическая деформация является результатом «скольжения» плоскостей. Последнее связано с движением дислокации, которая распространяется по всему кристаллу.
Таким образом, вещества, обладающие текучестью, вначале значительно удлиняются и подвергаются пластической деформации до момента разрушения. Их называют пластичными веществами, например, медь и кованое железо, являются пластичными. Если вещества, разрушаются сразу после достижения предела упругости — они называются хрупкими, например, стекло и высокоуглеродистые стали.
Латунь, бронза и многие сплавы не имеют предела текучести. Эти материалы увеличиваются в длине сверх этих пределов. Поскольку нагрузка растет без появления разрыва — эти материалы не подчиняются закону Гука.
Практическое применение
Очень важно понимать, при каких условиях выполняется закон Гука. Он работает только в упругом сечении металла, к которому применяется сила растяжения или сжатия. Механическое поведение материалов, позволяет сравнивать их деформационные способности в определенной среде, температуре и других характерных состояниях.
На практике его полезность проявляется главным образом в промышленной сфере и в строительной отрасли. Закон упругости и определение модуля Юнга также помогают оценить процесс разрушения материалов, например, в такой конструкции, как бетон. Они важны для исследования и разработки гибких и одновременно стойких материалов.
И позволяет прогнозировать влияние веса на строительные материалы, чрезвычайно полезен в областях: конструкционные материалы, автомобилестроение, кораблестроение, архитектура, строительство, энергетика и многие другие важные отрасли использующие механизмы.
Например, позволяет прогнозировать влияние веса автомобилей на мост и материалы, из которых он изготовлен. Наиболее известным применением закона упругости является разработка динамометров: устройств, которые позволяют измерять скалярную силу, состоящих из пружины и цифровой шкалы.
Пружины присутствуют практически во всех механизмах от бытовых приборов до тяжелого промышленного оборудования. Они являются накопителями механической энергии, их можно считать механическими аккумуляторами. Самые ранние пружинные часы появились в 1400-х.
Типы пружин и их применение:
- Пружина сжатия предназначена для работы со сжимающей нагрузкой и используются в амортизаторах, пружинных матрацах, механических карандашах и шариковых ручках.
- Пружина растяжения предназначена для работы с растягивающей нагрузкой. Они встречаются в багажных весах и механизмах гаражных ворот.
- Торсионная пружина предназначена для работы с крутящим моментом, скручивающая сила, усиливает каждую прищепку и мышеловку.
И также существует три класса пружин: пружины с линейной, с переменной скоростью, а также пружины с постоянной силой. Линейные пружины подчиняются закону Гука F=-К*Х. Формулировка означает, что сила, необходимая для растяжения или сжатия такой пружины на расстояние «Х», пропорциональна расстоянию, если сила не превышает предел упругости пружины.
Пружины кручения подчиняются аналогичной версии закона. В обоих случаях «К» — это скорость пружины, и она остается постоянной независимо от отклонения пружины. Вот почему линейные конструкции также известны как пружины с постоянной скоростью.
Пружины с переменной скоростью не имеет одинаковой скорости растяжения по всей осевой длине. Например, пружина сжатия в форме конуса, они устойчивы в поперечном направлении и менее подвержены деформации. Пружины постоянной силы установлены в часах. Этот тип пружины обычно представляет собой спиральную ленту из упругой стали.
Закон Гука стал основой раздела механики, получившего название теории упругости. Уже после открытия стало понятно, что закон может формулироваться для значительного перечня тел, поэтому имеет намного большую область применения. Атомы в твердом теле ведут себя таким образом, поскольку объединены между собой связями и при этом упруго зафиксированы в объемной кристаллической решетке.