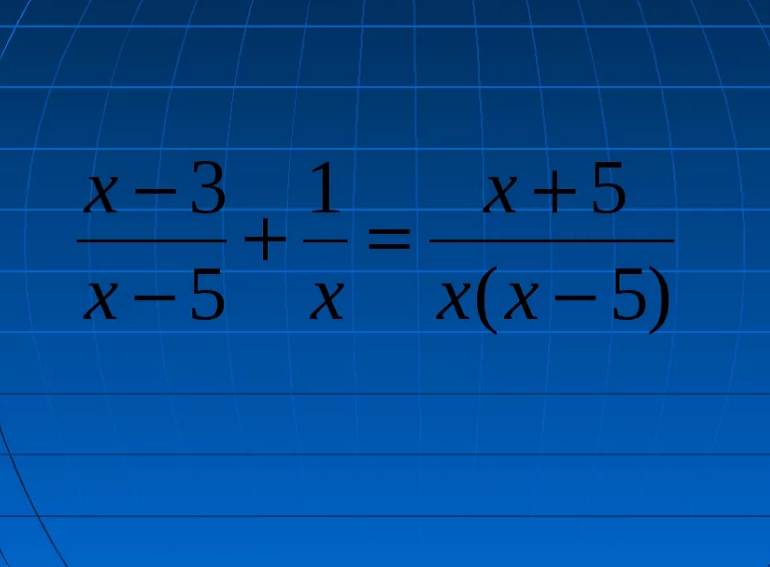Содержание
В алгебре все рациональные уравнения содержат рациональные выражения. Прежде чем дать определение, нужно выделить понятие рационального выражения.
Это не что иное, как запись, состоящая из переменного значения х и чисел, представленная с помощью арифметических действий: сложения, умножения, вычитания, деления, а также возведения в степень с натуральным показателем.
Что такое рациональные уравнения
Математики дают двоякое объяснение рациональному уравнению:
- Если обе части уравнения представляют собой рациональные выражения, такое уравнение является рациональным.
- Уравнение, в левой части которого рациональное выражение, а в правой стоит ноль, являются рациональным.

Например, алгебраическая запись следующего вида является рациональным уравнением:
2x − 12x2yz3 = 0.
Алгоритм решения рациональных уравнений

Чтобы решить уравнение из рассматриваемой темы, нужно сделать следующие шаги:
- Для начала потребуется все члены уравнения переместить в одну часть.
- Определить общий знаменатель.
- Следующим шагом определяются множители, на которые умножаются члены равенства и выполняется преобразование этой части уравнения к алгебраической дроби.
- Решается уравнение вида p(x) = 0.
- Для каждого найденного корня уравнения p(x) = 0 делается проверочное действие. Если выполняется условие q(x) ≠ 0, то это значение является корнем заданного уравнения. В противном случае значение признается посторонним корнем. Оно не включается в ответ.

Рациональные уравнения являются краеугольным камнем всего курса алгебры. Человеку, научившемуся работать с подобными выражениями, умеющему упрощать, раскладывать на множители, под силу решение любой задачи, ведь преобразование выражений — это одна из составляющих частей решения серьёзного уравнения или неравенства.
Основные алгебраические формулы
Для решения квадратных уравнений есть формулы и правила сокращённого умножения, которые начинают изучать уже в средних классах общеобразовательных школ:
- a2−b2=(a−b)(a+b) — разность квадратов.
- (a+b)2=a2+2ab+b2— квадрат суммы.
- (a−b)2=a2−2ab+b2— квадрат разности.
- a3+b3=(a+b)(a2−ab+b2) — сумма кубов.
- a3−b3=(a−b)(a2+ab+b2) — разность кубов.
Преобразования, упрощающие решение рациональных уравнений
Преобразования равносильны, если получается новое уравнение, причем корни будут такими же, как в изначальном выражении.
Деление или умножение уравнения на любое, отличное от нуля число, является равносильным преобразованием. Перенос параметров уравнения через знак равенства в ту или иную часть — тоже тождественное преобразование.
Примеры решений уравнений с дробями

Алгоритм решения следующий: все части приводятся к общему знаменателю. Но после того, как найдены корни при использовании неравносильных преобразований, они проверяются методом подстановки в уравнение.
Приведем дробь к такому виду:

С учетом всего этого получится выражение:

Методы решения
Наиболее часто используемые способы для решения уравнений со степенями:
- метод замены переменной;
- разложение на множители.

Биквадратные уравнения типа ax4 + bx2 + c = 0 решаются методом замены множителя: x2 = y.
Системы линейных уравнений также решаются методом замены.
К примеру, требуется решить систему линейных уравнений:

Принцип решения сводится к тому, что надо избавиться от лишней переменной:

Далее уравнение решается просто.
Пример решения с разложением на множители

Любые сложные вычисления нужно выполнять по действиям. Так проще избавиться от ненужных ошибок.
Алгоритм решения такой: вначале выполняется действие, заключённое в скобках, затем выполняется то, что записано во второй скобке и так далее. В конце все части объединяются, и находится результат.
Для самостоятельной работы при решении рациональных уравнений можно использовать онлайн-калькулятор. Он помогает лучше усвоить некоторые методы решения и быстрее справиться с заданиями.