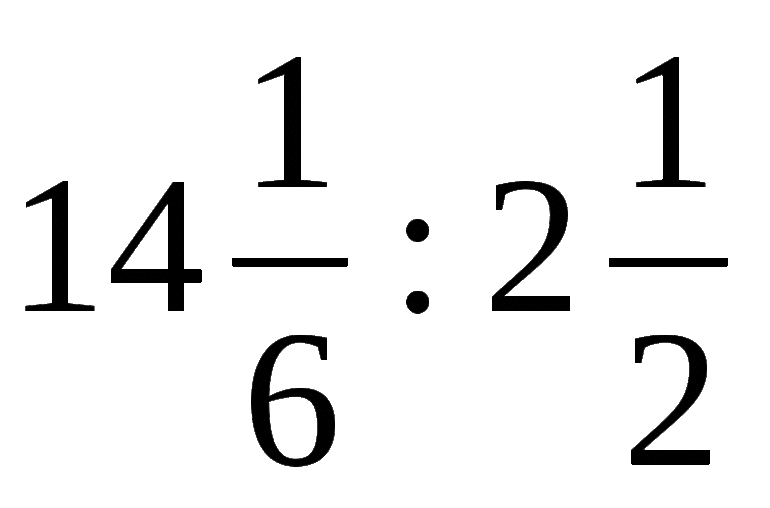Содержание
Выполнение операции нахождения частного двух дробных величин вызывает сложности у некоторых учеников при решении на уроках математики 5 класса примеров. Деление смешанных дробей считается очень сложным действием, поскольку необходимо постоянно выполнять преобразования. Специалисты разработали специальный алгоритм, позволяющий осуществлять эти действия правильно и без особых трудностей.
Общие сведения
При решении примеров по математике не всегда получаются целочисленные результаты. Это очень часто происходит при делении одного числа на другое. Следует отметить, что операция получения частного состоит минимум из трех элементов:
- Величины, которую нужно поделить — делимое.
- Числа, характеризующего количество равных частей, на которые требуется разделить делимое.
- Результата выполнения операции — частного.
Математическая форма записи имеет следующий вид: Q: T=Q/T=R, где Q — делимое, T — делитель и R — частное. Из формулы видно, что операция обозначается двумя способами: косой чертой «/» и двоеточием «:». Далее следует рассмотреть дробные выражения и их классификацию.
Классификация дробей
Дробные выражения — величины, которые не принадлежат к натуральным числовым значениям. Они бывают двух типов:
- Десятичными.
- Обыкновенными.
Первыми называются дроби, полученные при делении одного числа на другое и записанные в виде частного этих величин. Они состоят из целой и дробной частей, которые отделяются друг от друга запятой. Дробные тождества делятся на два вида: бесконечные и с фиксированным количеством знаков после запятой. Первые бывают периодическими (знаки после запятой повторяются через некоторый период) и непериодическими (нет закономерности повторения цифр).
Если дробь имеет фиксированное количество математических знаков (цифр), то ее называют конечной десятичной. Ее удобно записывать при расчетах различных величин. Однако бесконечные дробные выражения либо округляются, либо записываются в виде обыкновенных дробей. Последние бывают двух видов: правильными и неправильными.
Правильным обыкновенным дробным тождеством называется число, состоящее из числителя Q и знаменателя T при условии, что Q<Т. Примером правильной дроби является числовая величина 4/5, числитель которой равен 4, а знаменатель — 5. Кроме того, 4<5.
Неправильной дробью называется величина, состоящая из числителя Q и знаменателя T, но при этом должно соблюдаться условие Q>T. Примером такого значения является 5/4, так как 5>4. Следует отметить, что неправильная дробь, в отличие от правильной, имеет целую часть, и ее можно конвертировать в смешанное число.
Смешанные числа
Смешанное число — величина, состоящая из целой части и дробной, представленной обыкновенной дробью. Математическая форма записи имеет такой вид: P[Q/T], где Р — целое число, а Q/T — правильная обыкновенная дробь. Любую неправильную дробную величину можно превратить в смешанную величину. Для этой цели специалисты разработали такой алгоритм:
- Написать неправильное дробное выражение: Q’/T, где Q’>T.
- Найти целую часть при помощи деления с выделением целочисленной величины: Q’/T=Р.
- Вычислить по соотношению новый числитель неправильного дробного тождества. Он эквивалентен разности искомого числителя Q’ и произведения целой части на целое число: Q=Q’-PT.
- Записать искомое выражение смешанного дробного вида: Р[Q/T], где Q<T.
Однако для проверки правильности алгоритма и понимания его сути требуется разобрать преобразование на практическом примере с дробью неправильного формата 12/5. Конвертация осуществляется таким образом:
- Записать величину: 12/5.
- Выделить целое: 12/5=2.
- Новый числитель: 12−5*2=2.
- Результат: 2[2/5].
Если возникает необходимость конвертации смешанной величины в неправильную дробь, то математики рекомендуют воспользоваться обратной методикой. Она имеет следующий вид:
- Записать смешанное дробное значение: Р[Q/T].
- Найти числитель для неправильной дроби, который будет эквивалентен сумме искомого и произведения целой части на знаменатель: Q’=Q+PT.
- Написать результирующую величину с учетом нового числителя: Q’/T.
Специалисты считают, что любой алгоритм должен закрепляться на практическом примере, то есть необходимо решать задачу на преобразование смешанного выражения 2[2/5] в неправильную дробь. Реализация алгоритма выглядит следующим образом:
- Записать величину, которую нужно конвертировать: 2[2/5].
- Определить новый числитель по формуле: 2+2*5=12.
- Результат: 12/5.
Однако этих методик недостаточно, чтобы осуществить деление смешанных чисел. Для этого рекомендуется ознакомиться или повторить алгоритм получения частного для обыкновенных дробных выражений.
Правило деления
Делить смешанные дроби не так просто, когда неизвестна методика осуществления этой операции. Для этого нужно знать саму суть получения частного двух обыкновенных дробных тождеств. Специалисты рекомендуют запомнить такое правило: чтобы разделить одну дробь на другую, нужно первую умножить на обратную вторую.
Для некоторых учеников не совсем понятно значение термина «обратная». Это означает, что для 5/6 обратным значением является перевернутое значение, то есть 6/5. Алгоритм деления имеет такой вид:
- Записать две дроби с учетом знака деления в виде двоеточия (такая форма записи позволит не запутаться в операции): Q/T: R/S.
- Перевернуть вторую дробь, записав числовое выражение в новом виде: Q/T * S/R.
- Осуществить сокращение величин, а затем их перемножить: QS/TR.
Следует отметить, что иногда для уменьшения значений числителя и знаменателя рекомендуется выполнить сокращение. Это возможно, когда они содержат общие множители, то есть 3/6=(3*1)/(3*2), где тройка — общий множитель. Реализация алгоритма на практике для дробей 4/25 и 8/5 имеет такой вид:
- Записать операцию: 4/25: 8/5.
- Перевернуть вторую величину: 4/25 * 5/8.
- Сократить и записать результат: 4/(5*5) * 5/(2*4)=1/10.
Следует отметить, что сокращение нужно для облегчения дальнейших вычислений и упрощения выражения. Последнее действие является «правилом хорошего тона» в математике. Далее можно переходить непосредственно к алгоритму деления смешанных дробных чисел.
Алгоритм получения частного
Деление смешанных чисел похоже на операцию получения частного для двух дробей, но существуют некоторые нюансы. Чтобы их учесть, необходимо ознакомиться с алгоритмом, которым рекомендуют воспользоваться специалисты на начальной стадии обучения. Он имеет следующий вид:
- Записать две смешанные дроби с учетом операции деления.
- Выписать отдельно первое смешанное тождество и переконвертировать его в неправильную дробь.
- Аналогичную операцию выполнить и для второго элемента.
- Перевернуть вторую дробь неправильной формы, а также изменить знак деления на произведение.
- При необходимости выполнить сокращения.
- Перемножить числители и знаменатели.
- Записать результат.
На практике нужно разобрать деление двух смешанных чисел, то есть 2[8/12] 2[4/6]. Операцию необходимо выполнять по алгоритму. Его реализация имеет такой вид:
- Операция деления: 2[8/12]: 2[4/6].
- Первое смешанное значение: 2[8/12].
- Сокращение обыкновенной правильной дроби во втором пункте для оптимизации дальнейших вычислений: 2[2/3].
- Преобразование величины, полученной на третьем шаге, в обыкновенную дробь неправильной формы: (3*2+2)/3=8/3.
- Второе: 2[4/6].
- Упрощение выражения в пятом пункте: 2[2/3].
- Неправильная дробь: 8/3.
- Выполнение операции деления: 8/3: 8/3 = 8/3 * 3/8 = 1.
Следует отметить, что упрощение выражения можно производить на любом этапе, поскольку это действие не только помогает сделать расчеты более удобными, но и избежать ошибок при вычислениях и использования различных средств (калькулятора и компьютера).
Кроме того, величины 2[8/12] и 2[4/6] являются взаимообратными числами, поскольку их частное равно единице. Если бы такого результата не было (умножение обратных чисел), то в этом случае нужно перемножить числители и знаменатели двух дробных выражений, записав общий результат.
Таким образом, операцию деления смешанных чисел необходимо осуществлять по определенному алгоритму на начальных этапах обучения, поскольку этот подход позволит обучаться правильно. Кроме того, необходимо знать теорию о дробных значениях, их классификацию и методику получения частного значения.