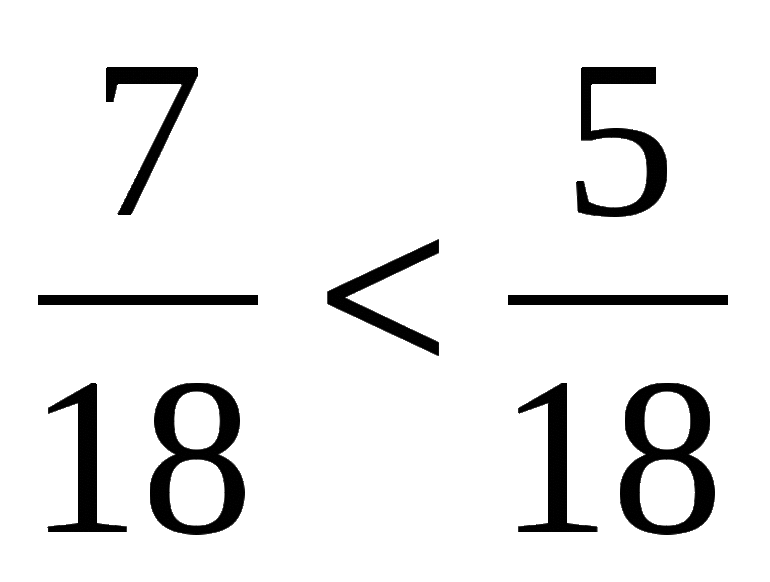Одним из фундаментальных знаний является в математике понятие дроби. Выражения начинают проходить в пятом классе. Школьников учат не только смыслу дробных чисел, но и выполнять над ними различные действия. При этом важно запомнить их основное свойство, часто довольно сильно упрощающее решения. Объяснение же лучше всего начинать с простого примера, доступного для понимания даже ребёнку.
Общие сведения
Ещё с давних времён у человека появилась потребность в счёте. Вначале это был простой делёж добычи. Затем люди стали выполнять измерения, считать объём, вес и время. Результат таких действий не всегда удавалось выразить целыми значениями. Для таких случаев числа начали дробить на части. Появились термины «треть», «половина», «четверть» и т. п.
Первое упоминание о дробях встречается в манускриптах Древнего Египта. В них указываются специальные символы в виде набора линий, обозначающих дробные выражения. Египтяне научились делить 2 предмета на троих, умножать и складывать нецелые числа. В Греции для их записи начали использовать разделяющую черту. Но современное обозначение в обиход ввели арабы. Появились такие записи в конце XII века.
Объяснить, что значит дробное выражение, проще всего на доступном примере. Пусть имеется буханка. Её можно описать как нечто целое. Если взять нож и разрезать изделие на 5 равных кусков, количественное значение не изменится. Можно всё так же утверждать, что есть одна буханка. Записывают такое действие как 5/5. Выражение обозначает, что целое было разделено на 5 частей, которые остались на месте.
Затем 2 куска съели. По факту на столе останется 3 кусочка от всей первоначальной буханки. Их ещё можно назвать долями. Каждый кусок занимает 1/5 от хлеба целиком, поэтому на столе осталось 3/5 от первоначального количества. Это изменение в математике произносят как три пятых, подразумевая, что после какого-то действия от целого осталась лишь определённая часть.
Современная запись дробного выражения включает 2 элемента:
- числитель (делимое) — показывает, сколько частей было забрано у целого;
- знаменатель (делитель) — определяет, на сколько долей разделили изначальное число.
Разделяет эти 2 значения черта. Называется она дробной и обозначает знак деления. Например, 3/8, здесь 3 — числитель, а 8 — знаменатель.
Таким образом, простое определение можно сформулировать так: дробью называют число, которое описывает операцию разделения целого на малые части. Над дробными выражениями можно не только выполнять различные арифметические операции, но и возводить в степень, находить логарифм, брать от них дифференциал.
Виды выражений
В зависимости от значения, которым обозначается дробное число, существует несколько записей выражений. В первую очередь, нужно отметить обыкновенную дробь. Это довольно простая запись, состоящая из двух натуральных чисел. Под последними понимают значения, возникающие естественным способом. Причём их множество неопределённо и считается бесконечным.
Обыкновенная дробь может быть трёх видов:
- правильная — выражение, в котором значение числителя меньше знаменателя (n/m, n<m);
- неправильная — запись числа, где делимое больше делителя (n/m, n>m);
- смешанная — дробь, в состав которой входит целое число и правильное выражение (k n/m).
Кроме обыкновенных дробей, существует ещё один класс — десятичные. Их особенность, что в знаменателе выражения всегда стоит число, кратное десяти. Существует даже специальная запись, подчёркивающая отношение дроби к этому типу. Выполняется она с помощью запятой, разделяющей целую часть от дробной. При этом запись можно выполнить и в классическом виде. Например, 1/10 или 0,1. Между двумя выражениями можно поставить знак равенства.
Естественно, между видами записей существует взаимосвязь. Смешанное число можно привести к неправильной дроби. Выражение вида 1 (2/3) представляет собой сумму целой части и отношения. Его можно переписать как сложение двух слагаемых 1 (2/3) = 1 + (2/3). Если выполнить операцию, получится дробь — 5/3. Любую неправильную дробь можно превратить в смешанную.
В 5 классе действия с дробями связаны именно с такими преобразованиями, поэтому стоит запомнить формулу: a (n / m) = (a * m + n) / m, и с её помощью выполнять превращения выражений. Алгоритм такого действия следующий:
- целую часть нужно умножить на знаменатель;
- с полученным числом сложить делимое;
- результат действия записать в числитель, а знаменатель оставить без изменения.
Чтобы превратить дробь в десятичную, нужно умножить на одно и то же число как числитель, так и знаменатель. Но подбирать его следует так, чтобы в делителе получилось выражение, кратное десяти.
Действия с дробями
С выражениями, записанными в виде отношений чисел, можно выполнять любые математические действия. Но перед тем как приступить к ним, следует проверить дробь на возможность сокращения. Выполнять упрощение можно, воспользовавшись основным свойством выражения.
Заключается оно в том, что значение дробного числа не изменится, если числитель и знаменатель умножить или разделить на одну и ту же величину, то есть справедливо выполнение следующих условий: a* m/b * m = a/b и (a: m)/(b: m) = a/b. Это замечательное свойство помогает упрощать сложные выражения, приводя их к простой записи. Например, 200/15. Числитель и знаменатель в этом случае можно разделить на 5: (200:5)/(15:5) = 40/3.
Алгоритмы выполнения основных операций с дробями :
- Умножение. Чтобы найти произведение двух дробей, нужно отдельно перемножить их числители и знаменатели: (a/b) * (n/m) = (a*n)/b*m).
- Деление. При нахождении частного двух дробей в выражении, которое выступает делителем, нужно поменять местами числитель со знаменателем, а затем найти произведение множителей: (a/b): (n/m) = (a/b) * (m/n) = (a*m)/(b*n).
- Сложение. Чтобы сложить 2 отношения, нужно их знаменатели привести к общему числу, а каждый числитель помножить на дополнительный множитель и выполнить сложение. Затем полученную сумму записать как делимое, а в делитель поставить общий знаменатель: a/b + c/n = ((a*n) + (c*b))/(b*n). Аналогичным образом выполняется вычитание. Только вместо суммы в числитель подставляется разность.
- Возведение в степень. Чтобы решить эту задачу, нужно отдельно возвести числитель и знаменатель: (a/b) n = an/bn.
Сами правила выполнения действий не слишком сложны. Единственно — следует подробнее рассмотреть нахождение общего знаменателя и дополнительных множителей. Чтобы определить, каким будет общий делитель, нужно выбрать большее число из стоящих в знаменателях, и попробовать его разделить на другое без остатка. Если действие выполняется, оно и будет искомым числом.
В ином случае выбранное значение умножают на 2 и вновь пробуют разделить. Затем на 3, 4 и так далее. Эту операцию повторяют до тех пор, пока удовлетворяющее условию число не будет найдено. Дополнительные множители находят делением общего знаменателя на каждый делитель.
Выполнять действия можно с любым количеством членов одновременно. Алгоритм вычислений при этом остаётся тем же.
Примеры с объяснениями
Дроби в 5 классе изучают в рамках школьной общеобразовательной программы. Но знать только в теории, как они решаются, мало. Необходимо уметь применять правила и на практике. Для этого следует решить несколько примеров самостоятельно. Причём начинать нужно с простых задач, переходя постепенно к заданиям высокого уровня сложности.
Вот некоторые из них, рассчитанные на учащихся пятых классов:
- На заводе по производству труб ¼ продукции изготавливается на экспорт. Какую часть составляют изделия, поступающие на внутренние рынки? Решение примера следует начать с анализа исходных данных. Общее количество труб можно принять за единицу. Чтобы решить задачу, нужно из неё вычесть экспортные изделия: 1 — (¼). Чтобы найти разность, следует вычислить общий знаменатель и дополнительные множители. В результате решение будет выглядеть так: 1 — (¼) = (1/1) — (¼) = ((1*4)/(1*4)) — ((1*1)/(4*1)) = (4—1)/4 = ¾.
- В классе учатся 20 школьников. Из них ¼ отличники, 5/20 хорошисты, а ½ составляют троечники. Определить число школьников каждой категории успеваемости. Решение выполняется в 3 действия. В первом можно найти количество отличников. Для этого общее число нужно умножить на известную часть: 20 * ¼ = 20/4 = 5. Аналогичные действия следует выполнить и для других категорий. Количество хорошистов составит: 20* 5/20 = 5; троечников — 20 * ½ = 10.
- В первый день продали 1/3, а за следующий ½ поступивших дынь. Найти, какую часть фруктов продали за 2 дня. Итак, всего было реализовано 5/6 дынь. Эта часть находится простым прибавлением: (1/3) + (½) = (2/6) + (3/6) = 5/6. Исходя из определения дроби, можно утверждать, что в магазин поступили 6 дынь. Тогда 1/3 это будет 2 штуки, а ½ — 3. Получается, что осталась одна дыня, а продано было 5 штук.
Таким образом, при решении задач нужно не только знать правила и алгоритмы, но и уметь анализировать условие. Этим и хороши дроби. Они учат школьников не только счёту, но и математической логике.